[vc_row columns_on_tablet=»keep»][vc_column h_text_align=»left» h_text_align_mobile=»left-on-mobile» v_align=»v-align-middle»][tm_textblock textarea_html_bkg_color=»#ffffff»]
El Número Fí
En la búsqueda de la perfección y de la belleza, los números han estado siempre ahí (como en todo) para, desde definirla hasta intentar crearla.
Hace un tiempo estuve bastante interesado en este tema, me documenté e intenté llegar a algo a través del uso del Número Áureo o Fí.
1,61803………. un número irracional (como PI) con infinitos decimales, Fi (la sexta letra del abecedario griego que equivale a nuestra F), Tau o Número Áureo. Ligado a la naturaleza, el número de oro (Áureo), también conocido como «La Proporción Áurea» compite hasta con el número PI en aplicaciones artísticas tanto pictóricas, esculturas, pasando incluso por musicales, como en las aplicaciones matemáticas para el desarrollo de aplicaciones 3D, etc. Su mayor utilización se remonta al siglo V a.C. donde a los griegos les sirvió para la construcción de edificios en los que debieran primar tanto la belleza como guardar proporcionalidad, no sólo con los elementos constructivos, sino que además, con el entorno. En Egipto, para la construcción de las pirámides, donde se destaca el primer uso del número Fi del que se tiene datos: la pirámide de Keops. Pero ahí no queda la cosa y en construcciones como la Torre Eifel podemos ver que sus proporciones se basan también en el Número Áureo.
Con la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, …), el número Fi aparece en el estudio del crecimiento proporcional de las plantas, en la formación «poliédrica» en los ojos de un insecto, en las celdas que componen una colmena, en el desarrollo de una caracola (el nautilus como ejemplo principal de estudios).

Para tener una pequeña idea del número Fi, sólo hay que mirar nuestras manos. La proporción entre las falanges de los dedos, es el Número Áureo. En el reino animal, la sucesión de Fibonacci se recoge claramente en las abejas, en su reproducción… Y así un larguísimo etcétera.
¿Que quieres más información porque te ha gustado? No tienes más que seguir leyendo 😉
El número áureo F es un número irracional, para obtenerlo procedemos de la siguiente manera:
Dado el segmento
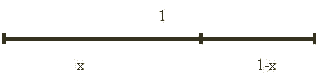
obtenemos la siguiente proporción:
(I)![]()
resolviendo la ecuación de segundo grado, obtenemos:
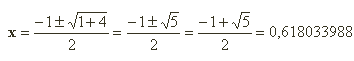
la solución con la raíz negativa no es valida y como F es la razón de la proporción (I), tenemos que F =1/x= 1,6180033988, al número 0,618033988 se le llama número áureo unitario y se le representa por la letra griega d.
(Explicación extraída de la página del Instituto de Tecnologías Educativas).
Supongo que todos conocemos el Hombre de Vitruvio de Leonardo Da Vinci, quien realizó este dibujo para ilustrar el libro «De Divina Proportione» del matemático Luca Pacioli editado en 1509. Para realizar la figura realizó todos los cálculos basándose en el Número Fi. Si se observa el dibujo, se pueden hacer 16 combinaciones de posturas de la figura. Como se puede ver, Leonardo Da Vinci no dejaba nada al azar ya que son 16 posturas, ni 15 ni 17, basándose en el Número Fí: 1,61803……….. No es nada casual. En todas sus obras (o la inmensa mayoría), las aplicación de Fí para las proporciones está más que estudiada. «La última cena», «La Gioconda»… etc.

¿Aplicaciones en la publicidad? Infinitas. Tenemos tan metida esa proporción debido a que socialmente está más que aceptada que nos sale casi sola. En cualquier aplicación, todo lo que se salga de una proporcionalidad similar al Número Áureo destaca de manera tanto positiva como negativa. Sólo hay que fijarse en cómo se estructuran la mayoría de los spots. Los encuadres, los planos, la iluminación… todo está estudiado al milímetro, quizás sin reparar en estas proporciones tan calculadas, pero sin duda con la influencia de esta «cultura de proporciones» que hemos «mamado» desde que nacemos.
En la creación y desarrollo de Identidad Corporativa está aún más presente. Todo es proporcional. Si observamos un DNI o una tarjeta de crédito, podemos ver que se trata del Rectángulo Áureo. Un rectángulo de proporciones perfectas cuyo desarrollo sería el siguiente:
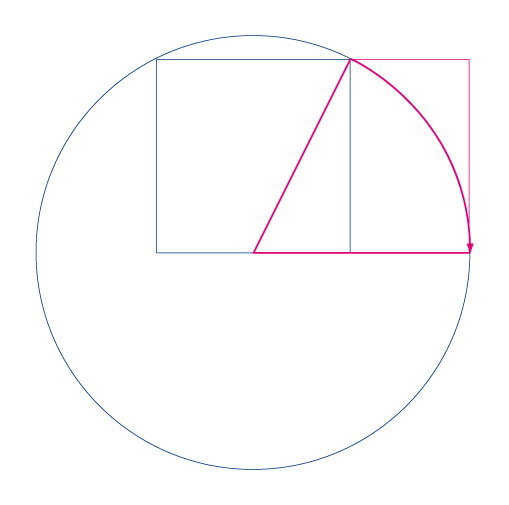
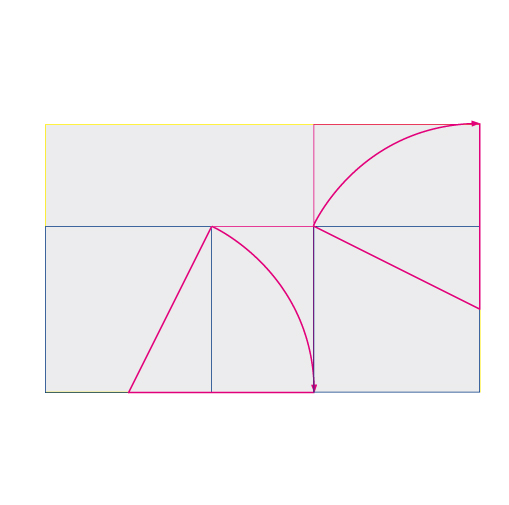
Observa cómo se puede crear, a partir del mismo, duplicándolo y girándolo 90º, dispuesto como en la imagen, un rectángulo de proporciones áureas mayor.
En la creación de tipografías, en la edición y diagramación, en la creación de libros… etc., etc.
En fin, un tema interesante ¿verdad? Pues a ver si alguien aporta más y seguimos aprendiendo.
[/tm_textblock][/vc_column][/vc_row]





